ЛАБОРАТОРНАЯ РАБОТА № 5
Классическое решение транспортных задач.
Цель работы: решение транспортных задач.
Общие сведения
Постановка транспортной задачи.
Имеется однородный груз и однородный тип подвижного состава. Груз
расположен в m пунктах А1, А2, …, Ai, …, Аm в количествах а1, а2, …, аi, …,
аm единиц. Есть заявки от n потребителей В1, В2, …, Вj, …, Вn на этот груз в
количествах b1, b2, …, bj, …, bn единиц. Имеется транспортная сеть, на
которой каждый поставщик может быть соединен с каждым потребителем
кратчайшим маршрутом (i, j), где i – номер (имя) поставщика, j – номер (имя)
потребителя.
В этой задаче будем считать известными заранее установленные
тарифы Cij денежных единиц на перевозку одной единицы груза от i-го
поставщика к j-ому потребителю.
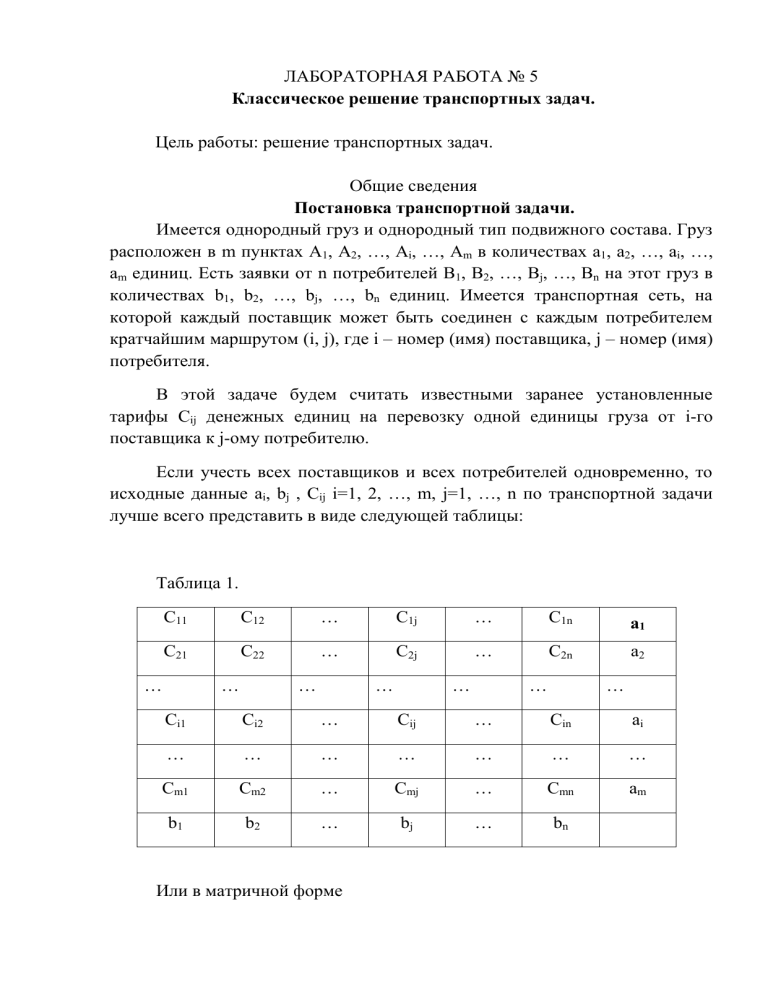
Если учесть всех поставщиков и всех потребителей одновременно, то
исходные данные ai, bj , Сij i=1, 2, …, m, j=1, …, n по транспортной задачи
лучше всего представить в виде следующей таблицы:
Таблица 1.
С11
С12
…
С1j
…
С1n
a1
С21
С22
…
С2j
…
С2n
a2
…
…
…
…
…
…
…
Ci1
Ci2
…
Cij
…
Cin
ai
…
…
…
…
…
…
…
Cm1
Cm2
…
Cmj
…
Cmn
am
b1
b2
…
bj
…
bn
Или в матричной форме
A=(a1, a2, …, am) запасы
B=(b1, b2, …, bn) заявки
С11, С12, …, C1n
С=
…
Сm1, Сm2, …, Cmn
Математическая модель транспортной задачи. Рассмотрим два
случая:
m
I.
n
a b
i
j 1
m
II.
j
, т.е. сумма запасов грузов равна сумме заявок
грузов (закрытая транспортная задача)
i 1
n
ai b j
, т.е. суммарных запасов больше, чем суммарных
заявок (открытая транспортная задача)
i 1
j 1
Закрытая транспортная задача.
Введем обозначения xij – количество груза, перевозимое от i-го
поставщика j-ому потребителю.
Так как количество возможных перевозок точно совпадает с
количеством маршрутов, то искомые перевозки xij лучше всего заменить в
виде рабочей таблицы размером (m+1)*(n+1)
Таблица 2.
1
…
1
2
...
x11
…
x1j
…
…
…
n
…
…
x1n
…
a1
…
xi1
…
xij
…
xin
ai
…
…
…
…
…
…
…
m
xm1
…
xmj
…
xmn
am
b1
…
bj
…
bn
Запишем условие задачи: Найти такой план (таблицу) перевозок
x11, x12, …, x1n
X=
…
xm1, xm2, …, xmn
m
n
F C ij x ij min
i 1 j 1
при котором функция
значения при следующих ограничениях:
достигнет минимального
n
x a i 1, m
ij
по вывозу i 1
i
m
x b
по ввозу i 1
ij
j
j 1, n
x ij 0, i 1, m, j 1, n
m
n
i 1
j 1
ai b j
Открытая транспортная задача.
m
n
ai b j
j 1
Если i 1
, то открытая транспортная задача сводится к закрытой
транспортной задаче путем ввода фиктивного потребителя с номером n+1 и с
объемом заявки равной
m
n
i 1
j 1
bn 1 a i b j
Если учесть, что этот условный потребитель не требует перемещения
самого груза и согласен его оставить в пункте поставки как остаток, то
тарифы по этому грузу Сi n+1 принимаются нулевыми, т.е. Сi n+1=0, i 1, m
В этом случае таблица открытой транспортной задачи в отличие от
таблиц 1, 2 закрытой транспортной задачи будет отличаться наличием
дополнительного столбца
Таблица 3
С11
…
С1n
0
a1
…
…
…
…
…
Cm1
…
Cmn
0
am
b1
…
bn
bn+1
x11
…
x1n
x1 n+1
a1
…
…
…
…
…
xm1
…
xmn
xm n+1
am
b1
…
bn
bn+1
Таблица 4
Транспортная задача решается средствами Excel с помощью процедуры
Поиск решения аналогично предыдущим задачам.
Задание на лабораторную работу.
Вариант №1
Найти оптимальный план перевозок.
Закрытая транспортная задача
А1=(26, 34, 22, 28)
Открытая транспортная
задача
А2=(50, 30, 10, 100)
В1=(31, 45, 12, 22)
В2=(31, 45, 12, 22)
6,8,3,1
8,9,4,2
C1
2,4,5,3
3,6,7,9
6,8,3,1
8,9,4,2
C2
2,4,5,3
3,6,7,9
Вариант №2
Найти оптимальный план перевозок.
Закрытая транспортная задача
А1=(22, 36, 26, 16)
Открытая транспортная
задача
А2=(20, 60, 20, 60)
В1=(25, 20, 44, 11)
В2=(25, 20, 44, 11)
3,6,5,2
4,6,2,3
C1
3,4,5,6
6,2,8,7
3,6,5,2
4,6,2,3
C2
3,4,5,6
6,2,8,7
Вариант №3
Найти оптимальный план перевозок.
Закрытая транспортная задача
А1=(52, 30, 65, 13)
Открытая транспортная
задача
А2=(80, 20, 60, 50)
В1=(27, 37, 47, 49)
В2=(27, 37, 47, 49)
7,8,4,6
9,10,5,1
C1
3,5,6,4
4,7,8,10
7,8,4,6
9,10,5,1
C2
3,5,6,4
4,7,8,10
Вариант №4
Найти оптимальный план перевозок.
Закрытая транспортная задача
А1=(24, 53, 48, 124)
Открытая транспортная
задача
А2=(50, 50, 50, 150)
В1=(85, 100, 37, 27)
В2=(85, 100, 37, 27)
9,7,6,4
8,6,4,3
C1
6,7,8,4
2,5,9,10
9,7,6,4
8,6,4,3
C2
6,7,8,4
2,5,9,10
Вариант №5
Найти оптимальный план перевозок.
Закрытая транспортная задача
А1=(15, 79, 44, 22)
Открытая транспортная
задача
А2=(30, 80, 70, 20)
В1=(55, 40, 26, 39)
В2=(55, 40, 26, 39)
10,8,5,4
9,12,3,5
C1
4,7,8,3
2,5,10,11
10,8,5,4
9,12,3,5
C2
4,7,8,3
2,5,10,11
Вариант №6
Найти оптимальный план перевозок.
Закрытая транспортная задача
А1=(22, 81, 44, 13)
Открытая транспортная
задача
А2=(20, 60, 20, 60)
В1=(37, 58, 26, 39)
В2=(37, 58, 26, 39)
5,6,1,5
7,9,3,8
C1
6,8,4,3
4,7,2,6
5,6,1,5
7,9,3,8
C2
6,8,4,3
4,7,2,6
Вариант №7
Найти оптимальный план перевозок.
Закрытая транспортная задача
А1=(47, 51, 14, 38)
Открытая транспортная
задача
А2=(50, 50, 60, 30)
В1=(25, 58, 45, 22)
В2=(25, 58, 45, 22)
6,5,3,2
8,9,4,3
C1
2,4,5,6
3,6,7,9
6,5,3,2
8,9,4,3
C2
2,4,5,6
3,6,7,9
Вариант №8
Найти оптимальный план перевозок.
Закрытая транспортная задача
А1=(24, 12, 15, 49)
Открытая транспортная
задача
А2=(30, 40, 10, 60)
В1=(27, 33, 22, 18)
В2=(27, 33, 22, 18)
2,4,5,8
9,6,5,7
C1
3,4,7,9
1,2,4,6
2,4,5,8
9,6,5,7
C2
3,4,7,9
1,2,4,6
Вариант №9
Найти оптимальный план перевозок.
Закрытая транспортная задача
А1=(15, 79, 44, 22)
Открытая транспортная
задача
А2=(30, 80, 70, 20)
В1=(55, 40, 26, 39)
В2=(55, 40, 26, 39)
10,8,5,4
9,12,3,5
C1
4,7,8,3
2,5,10,11
10,8,5,4
9,12,3,5
C2
4,7,8,3
2,5,10,11
Вариант №10
Найти оптимальный план перевозок.
Закрытая транспортная задача
А1=(24, 53, 48, 124)
Открытая транспортная
задача
А2=(50, 50, 50, 150)
В1=(85, 100, 37, 27)
В2=(85, 100, 37, 27)
9,7,6,4
8,6,4,3
C1
6,7,8,4
2,5,9,10
9,7,6,4
8,6,4,3
C2
6,7,8,4
2,5,9,10
