ТЕМА XX. КОНТУР С ТОКОМ
В МАГНИТНОМ ПОЛЕ
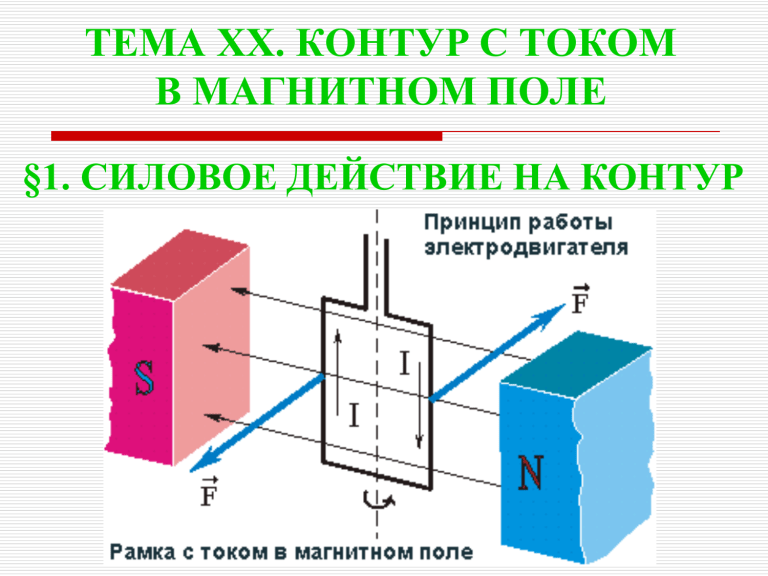
§1. СИЛОВОЕ ДЕЙСТВИЕ НА КОНТУР
1. МАГНИТНЫЙ МОМЕНТ
КОНТУРА С ТОКОМ
pm ISn;
pm IS ;
2
p
1
А
м
.
m
Магнитный момент контура определяет
магнитное поле контура в любой точке
и поведение контура в магнитном поле.
2. СИЛА, ДЕЙСТВУЮЩАЯ НА
КОНТУР В ОДНОРОДНОМ ПОЛЕ
По закону Ампера на элемент контура с током действует сила
dF I dl B .
Результирующая таких элементарных сил определяется
интегрированием вдоль всей длины контура
F I dl B .
L
В случае однородного поля
B const
F I dl B ;
L
dl 0 F 0.
L
3. НЕЗАВИСИМОСТЬ МОМЕНТА
СИЛ ОТ ТОЧКИ ОТСЧЕТА
Поскольку в однородном магнитном поле результирующая всех
сил равна нулю, то суммарный вращательный момент этих сил
относительно любой точки будет один и тот же. Докажем это.
Результирующий момент сил относительно некоторой точки О:
M r dF .
L
Выберем произвольную точку О’, cмещённую
относительно точки О на отрезок r0
r r0 r
r r r0 .
Результирующий момент сил относительно
точки О’ будет иметь вид:
M r dF r r0 dF
L
L
M r dF r0 dF M r0 dF M .
L
L
L
dF 0
L
4. МОМЕНТ СИЛ (МАГНИТНОЕ
ПОЛЕ В ПЛОСКОСТИ КОНТУРА)
dF1 IBdl1 sin 1 IBdy; dF2 IBdl2 sin 2 IBdy. dM IBdy x;
n B dM dM I n B dS .
M I n B dS I n B dS I n B S .
xdy dS dM IBdS ;
S
M ISn B pm B .
S
5. МОМЕНТ СИЛ (МАГНИТНОЕ
ПОЛЕ ПЕРПЕНДИКУЛЯРНО КОНТУРУ)
M dM r dF r I dl B I r dl B .
L
L
a b c b a c c (a b ) M I r B dl B r dl .
L
L
r B r B 0
M B(r dl ).
L
1
1
2
rdl rdr rdr d r M Bd r 2 ;
2
2L
B const
B
M d r 2 0.
2 L
6. МОМЕНТ СИЛ (ПРОИЗВОЛЬНОЕ
НАПРАВЛЕНИЕ ПОЛЯ)
B B B ;
B B sin ; B B cos .
M pm B pm B ;
M pm B pm B sin .
§2. РАБОТА И ЭНЕРГИЯ
В МАГНИТНОМ ПОЛЕ
1. ЭНЕРГИЯ КОНТУРА С ТОКОМ
В МАГНИТНОМ ПОЛЕ
При изменении угла
между векторами pm и
бесконечно малую величину d 0
магнитное поле совершит работу
B на
dA Md pm B sin d .
Работа сил поля совершается
за счёт убыли потенциальной
энергии контура с током в магнитном поле
dA dW dW dA dW pm B sin d .
Для нахождения конечного приращения энергии проинтегрируем
элементарные приращения
2
W2 W1 pm B sin d pm B cos 2 pm B cos 1
1
W pm B cos pm B.
2. УСТОЙЧИВОЕ И
НЕУСТОЙЧИВОЕ РАВНОВЕСИЕ
У контура с током в магнитном поле
два положения равновесия:
1 0 M 1 pm B sin 1 0;
2 M 2 pm B sin 2 0.
Первое положение равновесия
является устойчивым.
Это означает, что при отклонении
контура он возвращается в равновесие.
Второе положение равновесия неустойчиво.
Это ясно из энергетического анализа:
W1 pm B cos 1 pm B,
W2 pm B cos 2 pm B.
W2 W1
1 - уст. равновесие; 2 - не уст. равновесие.
3. КОНТУР С ТОКОМ В
НЕОДНОРОДНОМ ПОЛЕ
Рассмотрим неоднородное поле.
Направим ось x по направлению
градиента магнитного поля.
Поместим на оси x центра витка с током и направим
магнитный момент контура по внешнему полю.
Сила dF , действующая на элемент
dl , перпендикулярна к магнитной линии.
Поэтому силы, приложенные к различным
элементам контура образуют симметричный
конический веер. Равнодействующая этих сил
направлена в сторону возрастания поля B,
то есть втягивает контур в область сильного поля.
F W ( pm B)
B
B
B
F pmx
pmy
pmz
x
y
z
Fx pmx
B
.
x
4. ЭЛЕКТРОМАГНИТНОЕ
РУЖЬЕ
5. РЕЛЬСОТРОН
(РЕЛЬСОВЫЙ УСКОРИТЕЛЬ)
6. РАБОТА
МАГНИТНОГО ПОЛЯ
Жесткий (недеформируемый) контур с постоянным током перемещается
в магнитном поле. Выберем произвольный элемент контура dl .
Представим его произвольное бесконечно малое перемещение как
смещение параллельно самому себе на отрезок dh и поворот на угол d .
Тогда элемент контура опишет в пространстве поверхность площадью
dS:
1
2
dS dh dl d dl dh dl .
2
dA dF dh I dl B dh IB dh dl .
dh dl ndS dA IBndS IdФ.
dA dA IdФ IdФ.
L
2
L
2
A12 dA I dФ I Ф2 Ф1 .
1
1
