Дата 07.04.2020
Занятие № 76
Контрольную работу выполняем на двойных листах в клетку (листы
храним для сдачи на оценивание)
фото выполненной работы отправить для оценивания на адрес:
stt_matematika@bk.ru
Контрольная работа № 3 по теме «Прямые и плоскости в пространстве»
Выбор варианта по первой букве фамилии в алфавите (четная – нечетная
будет оценено
)
Вариант № 1
Параллельность прямых и плоскостей в пространстве
Часть 1. Задание с выбором ответа (1 балл).
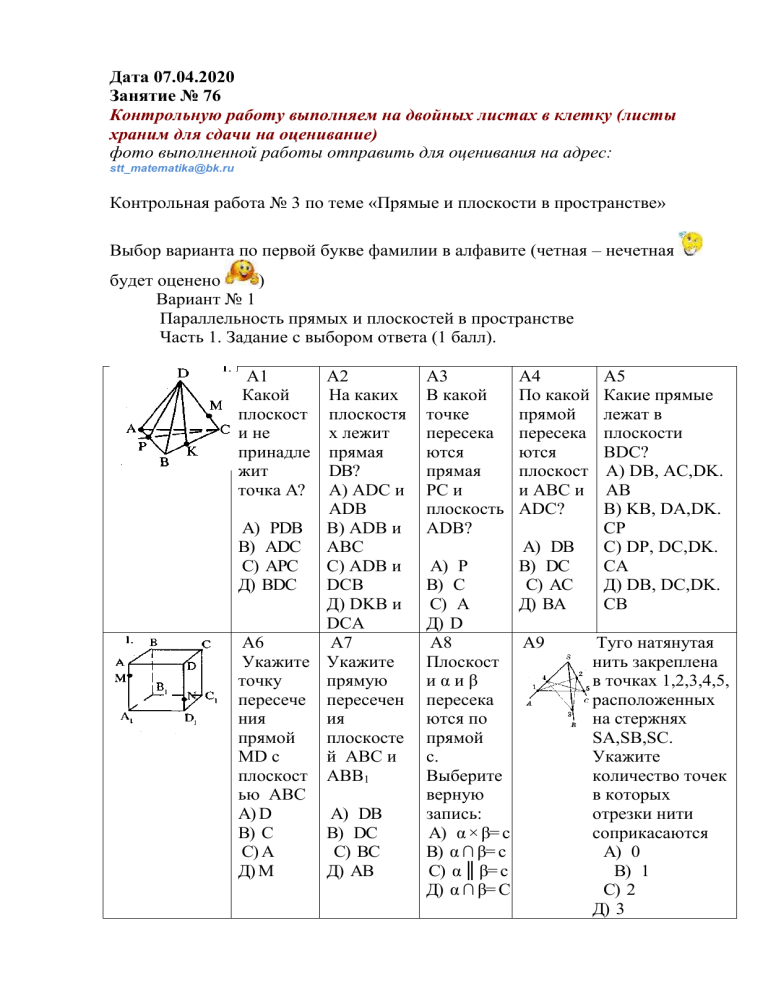
А1
А2
Какой
На каких
плоскост плоскостя
и не
х лежит
принадле прямая
жит
DB?
точка А? А) АDC и
ADB
А) РDВ В) ADB и
В) АDС ABC
С) АРС
С) ADB и
Д) ВDС
DCB
Д) DKB и
DCA
А6
А7
Укажите Укажите
точку
прямую
пересече пересечен
ния
ия
прямой
плоскосте
MD с
й АВС и
плоскост АВВ1
ью ABC
А) D
А) DВ
В) С
В) DС
С) А
С) ВС
Д) M
Д) AВ
A3
В какой
точке
пересека
ются
прямая
PC и
плоскость
ADB?
A4
По какой
прямой
пересека
ются
плоскост
и AВС и
ADC?
А) DВ
В) DС
С) АС
Д) ВA
А) Р
В) С
С) А
Д) D
А8
А9
Плоскост
иαиβ
пересека
ются по
прямой
с.
Выберите
верную
запись:
А) α × β= с
В) α ∩ β= с
С) α ║ β= с
Д) α ∩ β= С
A5
Какие прямые
лежат в
плоскости
BDC?
А) DB, AC,DK.
AB
В) KB, DA,DK.
CP
С) DP, DC,DK.
CA
Д) DB, DC,DK.
CB
Туго натянутая
нить закреплена
в точках 1,2,3,4,5,
расположенных
на стержнях
SA,SB,SC.
Укажите
количество точек
в которых
отрезки нити
соприкасаются
А) 0
В) 1
С) 2
Д) 3
А10
А11
А12
А13
Как
Найдите
Найдите Найдите рёбра,
располаг угол
точку
аются
между
пересечен
прямые
прямыми
ия
AD1 и
AD1 и ВВ1 прямых
D1C1?
А) 180º
DC и CC1
А)
В) 60 º
А) D
параллел С) 90 º
В) С
параллельные грани
ьны
Д) 45 º
С) А
АВВ1А1
В)
Д) К
А) АD, ВC, A1 D1, B1С1
пересека
В) АВ, ВC, A1 D1, B1С1
ются
С) DD1, CC1, C1 D1, DС
С)
перпенди
кулярны
Перпендикулярность прямых и плоскостей в пространстве
Часть 1. Задание с выбором ответа (1 балл).
А14
А15
А16
Укажите Выберите Как
рёбра,
верное
располож
перпенди утвержден ены друг
кулярные ие
к другу
плоскост А) AD║ BA рёбра
и АВВ1
В) AB D куба,
А17
А) DА,
выходящ
Отрезок ВD
1С1
ВC,СС1. С) DC ║ BC ие из
перпендикул
AB
Д) DС BC одной
ярен
В) СB,
вершины
плоскости α.
DA,D1А1.
?
СD является::
C1А1
А)
А)
С) DС,
Перпенд
Перпендику
ВC,DА.
икулярн
ляром
C 1В1
ы
В)
В)
Наклонной
Параллел
С)
ьны
Проекцией
наклонной
А18
А19
А20
Плоскост Прямые a и b параллельные
Укажи
и αиβ
и лежат в плоскости α.
те
параллель Через каждую из этих прямых
общий
ны.
проведена плоскость,
перпен
Каково
перпендикулярная α . Каково
дикуля
взаимное взаимное расположение
р для
прямы
х AD
и CC1
А) DС
В) СА
С) DD1
Д) ВС
расположе полученных плоскостей?
ние
А) Пересекаются
прямых
В) Скрещиваются
AD и BC? С) Параллельны
А)
Д) Совпадают
Пересека
ются
В)
Скрещив
аются
Часть 2. Задание с развёрнутым ответом (2 балла).
В3
Из точки М проведены к плоскости α до пересечения в точках N и К два
отрезка. Точки D и Е – середины отрезков MN и МК. Найдите длину отрезка NК,
если DЕ = 4 см.
С2
В7
Из точки О пересечения
Дан куб АВСDА1В1С1D1 ..
диагоналей квадрата АВСD к е го
Чему равен угол между
плоскости восстановлен
плоскостью А1В1С1D1 и
перпендикуляр ОМ так, что
плоскостью проходящей через
. Найдите косинус угла
прямые А1В1 и СD
АВМ.
В4
Через вершину острого угла
прямоугольного треугольника АВС с
прямым углом С проведена прямая АD,
перпендикулярная плоскости
треугольника. Чему равно расстояние от
точки D до вершины С, если АС = 6 см;
АD = 8 см.
С1
Из точки А к плоскости α проведены
два отрезка АС и АВ. Точка D
принадлежит АВ, точка Е принадлежит
АС. DЕ параллельна α и равна 5 см.
Найти длину отрезка ВС, если
.
С2
Из точки О пересечения
диагоналей квадрата АВСD
к е го плоскости
восстановлен перпендикуляр
ОМ так, что
.
Найдите косинус угла АВМ.
С3
С4
Из точки А построены три
В кубе со стороной а найдите
взаимоперпендикулярных отрезка
расстояние между прямыми ВD1 и
АВ, АС и AD. Найдите длину
СС1.
отрезка СD если АС = а, ВС = в, ВD
=с
Контрольная работа по стереометрии
Вариант № 2
Параллельность прямых и плоскостей в пространстве Часть 1.
Задание с выбором ответа (1 балл).
А1
Какой
плоскости
не
принадле
жит точка
В?
А) РDВ
В) АDС
С) АРС
Д) ВDС
А6
Укажите
точку
пересечен
ия прямой
NC1 с
плоскость
ю A1B1C1
А) D1
В) С1
С) А 1
Д) В1
А2
На каких
плоскостях
лежит прямая
DА?
А) АDC и ADB
В) ADB и ABC
С) ADB и DCB
Д) DKB и DCA
А7
Укажите
прямую
пересечения
плоскостей
АВD и АDD1
А) DВ
В) ВВ1
С) ВС
Д) AD
A3
В какой
точке
пересека
ются
прямая
DК и
плоскость
ADB?
А) Р
В) К
С) А
Д) D
А8
Прямые а
иb
пересека
ются в
точке С.
Выберите
верную
запись:
А) a ×b= с
В) a ∩ b= с
С) a║ b= с
Д) a∩ b= С
A4
По какой
прямой
пересека
ются
плоскост
и AВС и
ADВ?
А) DВ
В) DС
С) АС
Д) ВA
А9
A5
Какие прямые
лежат в
плоскости
BDА?
А) DB, AC,DK.
AB
В) KB, DA,DK.
CP
С) DP, DВ,DА.
ВA
Д) DB, DC,DK.
CB
Туго
натянутая
нить
закреплена в
точках
1,2,3,4,5, 6
расположенн
ых на
стержнях
SA,SB,SC.
Укажите
количество
точек в
которых
отрезки нити
соприкасают
ся
А) 0 В) 1
С) 2
Д) 3
А10
Как
располага
ются
прямые
DD1 и
DC?
А)
параллель
ны
В)
пересека
ются
С)
перпенди
кулярны
А11
Найдите угол
между
прямыми AА1 и
ВС
А) 180º
В) 60 º
С) 90 º
Д) 45 º
А12
Найдите
точку
пересечен
ия
прямых
DC и D1P
А) D
В) С
С) А
Д) К
А13
Найдите рёбра,
параллельные грани
АDD1А1
А) ВС, CC1, ВВ1, B1С1
В) АВ, ВC, A1 D1, B1С1
С) АD, ВC, A1 D1, АС
Перпендикулярность прямых и плоскостей в пространстве Часть 1.
Задание с выбором ответа (1 балл).
А14
А15
А16
А17
Укажите Выберите
Можно ли
Отрезок ВD
рёбра,
верное
провести
перпендику
перпенди утверждение
плоскость
лярен
кулярные А) AD BA
В) через
плоскости
плоскости AB D 1С1
четыре
α. СВ
АВС
произвольн
является::
А) DА,
С) DC ║ BВ1 Д) ые точки
А)
ВC,СС1.
DС BC
пространств
Перпендику
AB
а?
ляром
В) СB,
А) Да
В)
DD1,D1А1.
В) Нет
Наклонной
C1А1
С)
С) АА1,
Проекцией
ВВ1,DD1.
наклонной
C 1 С1
А18
А19
А20
Укажите
Плоскости α и β
Прямые a и bобщий
параллельны. Каково скрещивающиеся.Через
перпенди
взаимное
а проведена плоскость α
куляр для
расположение
║ b,. Через прямую b
прямых
прямых AС и BD?
проведена плоскость β║а, .
AВ и CC1
А) Параллельны
Каково взаимное
А) DС
В) Скрещиваются расположение плоскостей α
В) СА
и β?
С) DD1
А) Пересекаются
Д) ВС
В) Скрещиваются
С) Параллельны
Д) Совпадают
Часть 2. Задание с развёрнутым ответом (2 балла).
В1
Через концы
отрезка MN
и его
середину К
проведены
параллельны
е прямые,
пересекающи
е плоскость
α в точках M
1, , N1 и К1 .
Найдите длину
отрезка КК1 ,
если отрезок
MN не
пересекает α
и ММ1 = 12см,
NN1= 4 см.
В4
В5
Через вершину
Наклонная
острого угла
равна 2 см.
прямоугольного Чему равна
треугольника
проекция
АВС с прямым этой
углом С
наклонной
проведена
на
прямая АD,
плоскость,
перпендикулярн если
ая плоскости
наклонная
треугольника.
составляет с
Чему равно
плоскостью
расстояние от
угол равный
точки D до
60 º?
вершины С, если
АС = 3 см; АD =
4 см.
В2
В3
Даны две
Из точки М проведены
параллельные
к плоскости α до
плоскости.
пересечения в точках N
Через точки А и и К два отрезка. Точки
В одной из
D и Е – середины
плоскостей
отрезков MN и МК.
проведены две Найдите длину отрезка DЕ
параллельные
, если NК = 4 см.
прямые до
пересечения в
точках А1 и В1.
Найдите длину
отрезка АА1
если ВВ1 = 16
см.
В6
В7
Отрезки
Дан куб
двух
АВСDА1В1С1D1 ..
наклонных, Чему равен угол между
проведённы плоскостью А1В1С1D1 и
е из одной плоскостью
точки до
проходящей через
пересечени прямые АВ и С1D1
яс
плоскостью
, равны 7 и
10 см,
проекция
одного из
отрезков
равна 8 см.
Найдите
проекцию
другого
отрезка.
Часть 3. Задание с развёрнутым ответом (3 балла).
С1
С2
С3
С4
Из точки А Из точки О
Из точки А построены В кубе со
к плоскости пересечения
три
стороной
α проведены диагоналей
взаимоперпендикулярн а найдите
два отрезка
квадрата АВСD
ых отрезка АВ, АС и расстояни
АС и АВ .
к е го плоскости AD. Найдите длину
е между
Точка D
восстановлен
отрезка ВD если АС = прямыми
принадлежит перпендикуляр
а, ВС = в, СD = с
В1D и
АВ, точка Е ОМ так, что
АА1.
принадлежит
.
АС. DЕ
Найдите косинус
параллельна α угла АВМ.
и равна 5 см.
Найти длину
отрезка ВС,
если
.
Варианты имеют одинаковый уровень сложности и содержат
20 заданий с выбором ответа, каждое из которых оценивается 1б,
7 заданий с кратким ответом, каждое из которых оценивается 2б,
4 задания с развёрнутым ответом, каждое из которых оценивается 3б.
Критерии оценивания
«5» выставляется, если студент набрал 37 – 46 баллов.
«4» выставляется, если студент набрал 27 – 36 балл.
«3» выставляется, если студент набрал 19 – 26 баллов.
«2» выставляется, если студент набрал менее 19 баллов.
