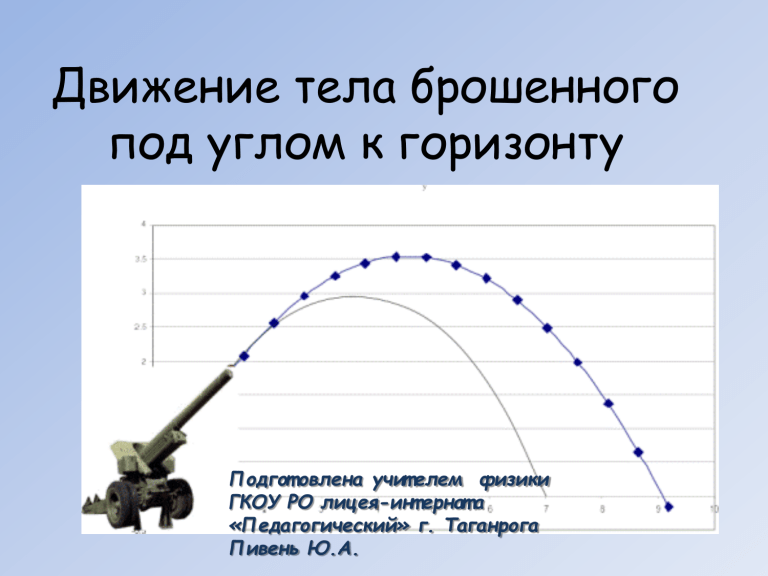
Движение тела брошенного
под углом к горизонту
Подгот овлена учит елем физики
ГКОУ РО лицея-инт ернат а
«Педагогический» г. Таганрога
Пивень Ю.А.
Движение тела брошенного
под углом к горизонту
Содержание
• Проекции векторов на координатные
оси.
• Постановка задачи
• Уточнение задачи
• Решение задачи
Проекция вектора на
координатную ось
Что называют проекцией вектора на
координатную ось?
X
Длину отрезка между проекцией начала
и конца вектора на координатную ось
называют проекцией вектора на координатную ось.
Проекция вектора
на координатную ось
Вспомним некоторые случаи
нахождения проекций.
X
Проекция вектора на
координатную ось
Вспомним некоторые случаи
нахождения проекций?
X
Проекция вектора на
координатную ось
Вспомним некоторые случаи
нахождения проекций.
X
Проекция вектора на
координатную ось
Общий случай. Угол наклона вектора не
равен 0 и 90 градусов.
X
Проекция вектора на
координатную ось
Общий случай. Угол наклона вектора
не равен 0 и 90 градусов.
X
Движение тела под действием
силы тяжести.
Задача. Решить основную задачу механики
для тела брошенного с начальной
скоростью v0 под углом к горизонту α
Дано:
v0
α
Расставим векторы скорости
и ускорения
α
Уточнение условия задачи.
В чем заключается основная задача
механики?
Определение
Определение положения
положения тела
тела вв любой
любой
момент
момент времени.
времени. x(t),
x(t), y(t)
y(t)
Под
Под действием
действием какой
какой силы
силы двигается
двигается тело
тело
брошенное
брошенное под
под углом
углом кк горизонту?
горизонту?
Под действием силы тяжести.
Какое ускорение сообщает сила тяжести
сообщает всем телам? Как оно
направлено?
Ускорение свободного падения g=9,8 м/с2 .
Направлено вертикально вниз.
Решение задачи.
Так как тело движется с ускорением свободного
падения, то искать решение будем исходя из
уравнения равноускоренного движения.
Почему для описания движения тела
брошенного под углом к горизонту нужно
два уравнения?
Решение задачи.
Найдем проекции начальной скорости и ускорения
на координатные оси.
y
α
x0=0,
y0=0
x
Решение задачи.
Подставим полученные значения в уравнения
движения тела брошенного под углом к горизонту
x0=0,
y0=0
Получим уравнение траектории.
Для этого из уравнений координат
исключим время: t = X
V0 cos α
a=
x
gx 2
y = V0
x sin α
2
2
V0 cos α
2V0 cos α
Введём обозначения:
Тогда получим: y = ax 2 + bx
Если начальная высота h0 не равна
нулю: y = ax 2 + bx + c
Это уравнение параболы.
Таким образом, уравнение
траектории движения тела, брошенного
под углом к горизонту, представляет
собой уравнение параболы, обращённой
ветвями вниз.
Время подъёма:
Время всего полёта
Максимальная высота
подъёма
Максимальная дальность
полёта
