ОБЩИЕ МЕТОДИЧЕСКИЕ УКАЗАНИЯ
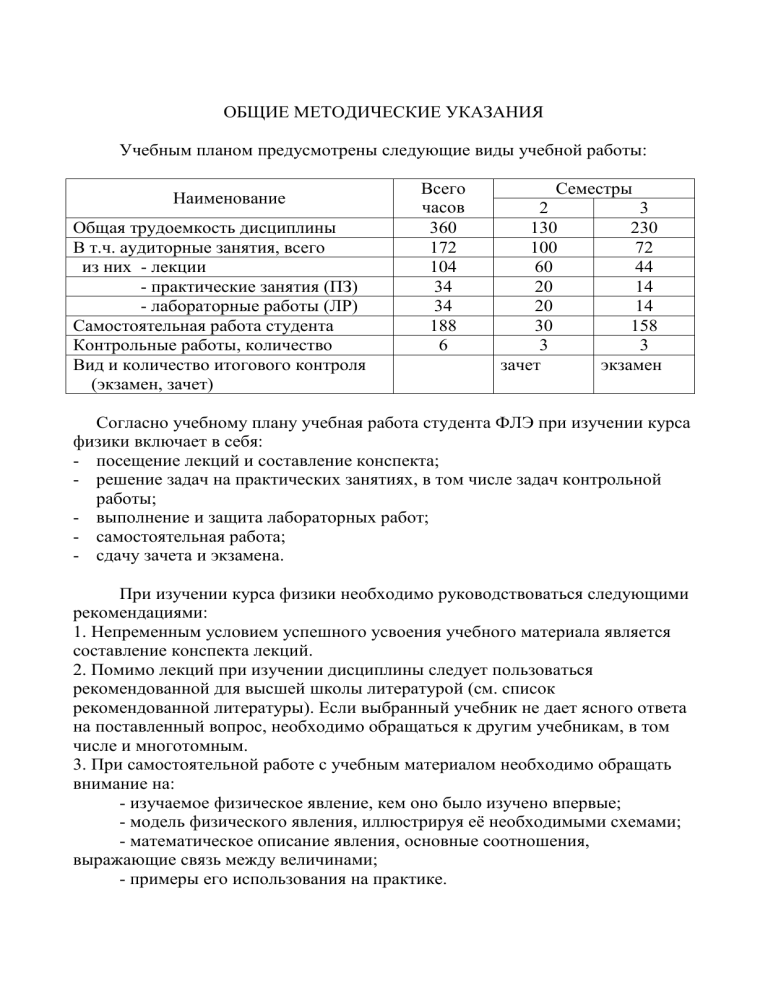
Учебным планом предусмотрены следующие виды учебной работы:
Наименование
Общая трудоемкость дисциплины
В т.ч. аудиторные занятия, всего
из них - лекции
- практические занятия (ПЗ)
- лабораторные работы (ЛР)
Самостоятельная работа студента
Контрольные работы, количество
Вид и количество итогового контроля
(экзамен, зачет)
Всего
часов
360
172
104
34
34
188
6
Семестры
2
130
100
60
20
20
30
3
зачет
3
230
72
44
14
14
158
3
экзамен
Согласно учебному плану учебная работа студента ФЛЭ при изучении курса
физики включает в себя:
- посещение лекций и составление конспекта;
- решение задач на практических занятиях, в том числе задач контрольной
работы;
- выполнение и защита лабораторных работ;
- самостоятельная работа;
- сдачу зачета и экзамена.
При изучении курса физики необходимо руководствоваться следующими
рекомендациями:
1. Непременным условием успешного усвоения учебного материала является
составление конспекта лекций.
2. Помимо лекций при изучении дисциплины следует пользоваться
рекомендованной для высшей школы литературой (см. список
рекомендованной литературы). Если выбранный учебник не дает ясного ответа
на поставленный вопрос, необходимо обращаться к другим учебникам, в том
числе и многотомным.
3. При самостоятельной работе с учебным материалом необходимо обращать
внимание на:
- изучаемое физическое явление, кем оно было изучено впервые;
- модель физического явления, иллюстрируя её необходимыми схемами;
- математическое описание явления, основные соотношения,
выражающие связь между величинами;
- примеры его использования на практике.
РЕКОМЕНДОВАННАЯ ЛИТЕРАТУРА
а) основная литература:
1. Трофимова Т.И. Курс физики. М., Высшая школа, 1998 и последующие годы
издания.
2. Савельев И.В. Курс общей физики. М., Наука, 1978 и последующие годы
издания.
3. Волькенштейн В.С. Сборник задач по общему курсу физики. М., Наука, 1975 и
последующие годы издания.
б) дополнительная литература:
1. Гусев В.Г., Павлов С.С, Сипаров С.В. Сборник задач по физике.
СПБ, АГА, 2000 г.
2. Гусев В.Г. Физика. Справочное пособие по разделам:
- основы механики;
- основы молекулярной физики и термодинамики;
- основы электродинамики.
СПБ, СПб ГУГА, 2009 г.
3. Гусев В.Г. Физика. Справочное пособие по разделам:
- основы теории колебаний и волн, основы волновой оптики;
- основы квантовой физики, основы атомной физики;
- основы физики атомного ядра и элементарных частиц.
СПБ, СПб ГУГА, 2010 г.
4. Арбузов В.И. и др., Физика. Методические указания по выполнению
лабораторных работ/ Университет ГА. С.-Петербург, 2013.
Методические рекомендации к решению задач на практических
занятиях и при выполнении контрольных работ
1. Решение любой задачи должно содержать:
- краткую запись условия задачи;
- эскиз;
- ссылки на используемые законы, правила, определения;
- последовательное решение задачи в общем виде, приводящее к
получению рабочей формулы, и запись окончательного ответа.
2. В некоторых задачах требуется определить величину (модуль) вектора.
Величина (модуль) вектора – по определению положительное число, равное
длине вектора. Поэтому если в задаче надо найти величину импульса тела,
силы или другой векторной характеристики, то ответ не может быть
отрицательным.
3. Численные значения следует подставлять в рабочую формулу после
решения задачи в общем виде.
4. При подстановке физических постоянных и иррациональных чисел
рекомендуется для упрощения вычислений использовать следующие значения:
- ускорение свободного падения ………… g 10 м / с 2 ,
- универсальная газовая постоянная …… R 8,3 Дж/ моль К ,
- коэффициент в законе Кулона …………
1
4 0
9 10 9 м / Ф ,
- скорость света в вакууме ……………… с 3 108 м / с ,
- постоянная Планка ……………………… h 6,6 1034 Дж с ,
- электрон–вольт ………………………….. 1 эВ 1,6 1019 Дж ,
- заряд электрона ………………………….. е 1,6 1019 Кл ,
- число Авогадро ………………………….. N A 6 1023 1/ моль ,
- плотность воды …………………………… 1000 кг / м3 ,
- молярная масса водорода………………… 0,002 кг / моль ,
- молярная масса гелия …………………….. 0,004 кг / моль ,
- удельная теплоемкость воды…………….. c уд 4200 Дж / кг К ,
2 1,41;
3 1,73 .
- 3,14;
5. Ответ следует приводить в системе СИ, если в условии задачи
отсутствуют особые указания. Ответы проставляются с указанием единиц
измерения в виде целого числа или конечной десятичной дроби.
Например: 210 Дж; 55 мкКл, 40 нФ, 0,65 с; 75,4 Н.
6. При решении задачи целесообразно придерживаться следующей
последовательности действий:
- внимательно прочитать задачу и понять ее смысл.
- записать кратко условие задачи и произвести перевод значений заданных
физических величин в систему СИ.
- сделать эскиз или схему, поясняющую содержание задачи. Это особенно
важно при решении задач, где используются векторные величины.
- подумать, какими физическими понятиями, законами, соотношениями надо
воспользоваться.
- решить задачу в общем виде и получить рабочую формулу (т. е. выразить
искомую величину через данные в условии задачи).
- подставить числовые значения и провести вычисления.
- записать ответ с указанием размерности в требуемых единицах.
ПРИМЕРЫ РЕШЕНИЯ ЗАДАЧ
Задача № 1
Угол при основании наклонной плоскости (НП) равен 20 . Тело массой 5 кг движется по НП с коэффициентом
трения 0,1. Определить:
1) длину НП, чтобы скорость тела в конце НП была равна 8 м/с;
2) работу силы тяжести при движении тела по НП.
Дано:
20
m 5 кг
тр 0,1
Общий план решения:
1. Эскиз с указанием систем отсчёта и сил, действующих на тело.
2. Уравнение движения тела по НП.
3. Основные кинематические соотношения.
4. Выражение для работы.
B 8 м / с
y
N
LНП ?
Amg ?
Fтр
α
x
mg
1. Уравнение движения в векторной форме:
ma mg N Fтр
(1)
2. Уравнения движения в проекциях на координатные оси:
max mg sin 0 Fтр
OX:
(2)
Fтр тр N
OY:
ma y mg cos N 0
(3)
a y 0 , т. к. НП – ровная.
N mg cos ; Fтр тр mg cos
(4)
Выражение (2) с учётом соотношений (4) можно переписать:
max mg cos тр mg cos
Ускорение, с которым тело движется по НП, равно:
ax g sin тр g cos
Численное значение ускорения
ax 10 0,342 0,1 10 0,939 3,42 0,94 2,48 м / с 2
Значение sin è cos найдём с помощью калькулятора.
(5)
3. При равноускоренном движении
x ax t ,
axt 2
2
Sx
tB
след.,
B
ax
8
3,2 c
2,48
t2
3,22
S B ax B 2,48
12,69 12,7 м,
LНП 12,7 м
2
2
4. По определению, работа силы равна AF F r cos ,
( F ^ r ) .
В конкретном случае:
F mg 5 10 50 H ,
90 90 20 70
r LНП 12,7 м,
Работа силы тяжести:
Amg mg LНП cos 50 12,7 0,342 217 Дж
Ответ: LНП 12,7 м.
Amg 217 Дж
Определить концентрацию и среднюю квадратичную скорость атомов гелия, который находится в
баллоне объёмом 3 л при давлении 1,5 атм. и температуре 20 .
Общий план решения:
1. Уравнение Клапейрона-Менделеева.
2. Основное уравнение МКТГ.
Дано:
СИ:
г
моль
V 3 дм3
3 10 3 м3
p 1,5 атм
1,5 10 Па
t 20 C
293 К
He 4
n?
кв ?
Определим число молей и число атомов тела в баллоне:
5
pV
; N NA
RT
Концентрация атомов гелия:
N N A pV N A N A p
p
V
V
RT V
R T kT
5
1,5 10
n
3,7 10 25 м 3
23
1,38 10 293
n
Исходя из основного уравнения МКТГ
1
р n m0 кв2
3
Найдём значение средне квадратичной скорости:
кв
3р
3 рV
3RT
3RT
n m0
3 8,31 10 3 293
кв
1350 м / с
4
25
3
Ответ: n 3,7 10 м ; кв 1350 м / с
Зад
ача
№
2
Задача № 3
Два точечных заряда -4 мкКл и 8 мкКл находятся на расстоянии 0,21 м друг от друга. На каком
расстоянии от первого заряда находится точка, в которой потенциал поля от двух зарядов равен
нулю? Найти напряжённость поля в данной точке.
Дано:
q1 4 мкКл 4 10 6 Кл
q2 8 мкКл
r0
6
8 10 Кл
xМ
r0 0,21 м
q1
М 0
q2
Е 1 Е2 M
xМ ?
Общий план решения:
1. Принцип суперпозиции.
2. Потенциал точечного заряда, системы двух зарядов.
3. Напряженность точечного заряда, системы двух зарядов.
EМ ?
Принцип суперпозиции.
Поля, созданные различными заряженными телами, не зависят друг от друга и накладываются друг
на друга.
рез 1 (q1 ) 2 (q 2 );
E рез E1 (q1 ) E (q 2 )
Потенциалы полей точечных зарядов в точке М:
1 (q1 )
kq1
;
xм
2 (q1 )
kq2
;
r0 xм
k
1
4 0
kq
kq2
0
По условию задачи: ì 0 , таким образом 1
x м r0 xМ
Получим алгебраическое соотношение, содержащее неизвестную величину xМ в первой степени.
q1r0
4 10 6 0,21 0,21
Находим xМ
0,07 м
q1 q2 (4 8) 10 6
3
Знак «-» при нахождении x ì не надо учитывать, т. к. он учтён раньше при нахождении потенциала
от первого заряда.
Напряжённость поля в точке М от зарядов q1 и q2 соответственно равны:
E1
kq1
kq2
; E2
.
2
xм
(r0 xм ) 2
E1
9 10 9 4 10 6
9 10 9 8 10 6
7340
кВ
/
м
;
E
3673 кВ / м
2
(7 10 2 ) 2
(14 10 2 ) 2
Напряжённость результирующего поля равна:
E
E E 11013 кВ / м
Задача № 4
Два литра воды от 10 C до температуры кипения в электрическом чайнике нагреются, за 15 минут.
Чайник работает от сети с напряжением 220 В и имеет КПД 60%. Определить сопротивление
нагревательного элемента и ток, протекающий по нему.
Дано:
V 2л
Масса воды в чайнике: m V
t1 10C
Теплота, затрачиваемая на нагревание воды: Qп С уд m t
t2 100 C
Теплота, выделившаяся при прохождении тока через нагревательный
U 220 В
0,6
15 мин
элемент: Qзатр
U 2
R
Коэффициент полезного действия нагревательного прибора:
R?
I ?
C уд Vt
U 2
R
Используя последнее выражение, найдём:
R
U 2
0,6 220 2 15 60
35 Ом
C уд Vt 4200 10 3 2 10 3 90
Ток, протекающий через нагревательный элемент, равен:
I
Ответ: R 35 Ом, I 6,3 А
U 220
6,3 А
R
35
Задача № 5
Электрон, пройдя ускоряющую разность потенциалов в 2000 В, попадает в магнитное поле с
индукцией B = 0,05 Тл и движется в нём по окружности. Определить импульс электрона и радиус
окружности траектории электрона.
Дано:
e 1,6 10
19
Общий план решения:
1. Движение частицы в электростатическом поле.
2. Движение частицы в магнитном поле.
Кл
m 9,11 10 31 кг
U 2000 В
B
B 0,05 Тл
В
FЛ
p?
Fлор
R?
R
R
+
2
ЭП
e
U
-
1
Электрон в электростатическом поле движется равноускоренно, т. к. на него действует
постоянная сила eE . Работа электростатического поля равна изменению кинетической энергии
электрона: A Wкин .
Записывая более подробно это соотношение, получим: eU
m 22 m12
.
2
2
Полагая, что скорость и кинетическая энергия электрона в начальном сечении 1 мала, получим:
2
2eU
m
2 1,6 10 19 2000
2,65 10 7 м / с 9,1 10 31
- с такой скоростью электрон влетает в магнитное поле, где на него действует сила Лоренца.
Уравнение движения частицы в магнитном поле имеет вид:
m 2
Be .
R
Сила Лоренца для электрона в магнитном поле выполняет роль центростремительной силы,
поэтому электрон движется по дуге окружности (или по полной окружности) радиуса
Be
.
m
24
кг м / с .
Модуль импульса электрона равен: p m 2emU 24,1 10
с центростремительным ускорением:
aцс
Радиус окружности, по которой движется электрон:
R
m
eB
Задача № 6
Колебательный контур состоит из катушки индуктивностью 1 мГн и воздушного конденсатора, обкладки
которого – две круглые пластины диаметром 20 см каждая. Расстояние между пластинами 1см. Определить
период колебаний контура и максимальное значение энергии конденсатора, если максимальное значение тока 2
мА.
Общий план решения:
1. Емкость конденсатора.
2. Период колебаний заряда, потенциала, тока для контура.
3. Закон сохранения энергии для колебательного контура,
энергия заряженного конденсатора.
Дано:
L 1 мГн
D 20 см
1 10 3 Гн
0,2 м
d 1см
0,01 м
I max 2 мА
2 10 3 А
T ?
C
L
Wэmax ?
I q
I
q
0
T/4
T/2
3T/4
T
t
Емкость плоского конденсатора зависит от его размеров и диэлектрической проницаемости среды.
Применительно к данной задаче:
S
D 2
4
, 1 (для воздуха),
C
0 S
d
0D 2
4d
Для идеального колебательного контура, используя формулу Томпсона, можно найти период
колебаний: T 2
L 0D 2
.
4d
LC 2
Численное значение периода колебаний равно:
T 2 3,14
1 10 3 1 8,87 10 12 3,14 0,22
10,5 10 7 с
2
4 1 10
Заряд конденсатора в идеальном колебательном контуре изменяется по гармоническому закону:
2 t
q qmax cos
.
T
При этом в моменты времени, когда t
nT
(n = 1,2,3,4….) заряд конденсатора принимает
2
максимальное значение, и в эти моменты времени энергия конденсатора достигает максимума. В
(2n 1)T
Задача № 7
Фокусное расстояние собирающей линзы 20 см, расстояние от предмета до линзы 10 см, высота
предмета 2 см. Найти высоту мнимого изображения. Как изменится высота изображения, если
предмет отодвинуть от линзы на расстояние 25. см?
Дано:
F 20 см
d 10 см
h 2 см
d1 25 см
Общий план решения:
1. Эскиз хода лучей для первого и второго случая.
2. Формула тонкой линзы.
H ?
H1 ?
f
H
F
F
H1
d
d1
f1
На одном эскизе показаны положение предмета и изображения и их геометрические размеры:
для первого ( d , f , h, H ) и второго ( d1 , f1 , h, H 1 ) случая.
В первом случае, когда d F , изображение предмета - мнимое увеличенное.
1 1 1
, находим расстояние до изображения:
F d f
dF
f
H
f
, а затем, используя соотношение:
, определяем высоту мнимого
d
h
F d
Fh
изображения: H
.
F d
20 2
4 см .
Высота мнимого изображения равна: H
20 10
Из формулы тонкой линзы
Во втором случае, когда предмет отодвинули от линзы на 25 см, и он стал расположен между F и
2F, изображение предмета будет действительным увеличенным.
Формула тонкой линзы в этом случае имеет вид:
Расстояние до изображения равно: f1
1
1
1
.
F d1 f1
Fd 1
.
d1 F
Высота действительного изображения будет равна: H1
Fh
20 2
8 см .
d F 25 20
Задача № 8
Электрическая лампа мощностью 150 Вт излучает 1,2% потребляемой энергии в видимой
области спектра. Сколько фотонов видимого света с длиной волны 550 нм ежесекундно
попадает в зрачок человека, находящегося на расстоянии 1 м от лампы? Диаметр зрачка – 4 мм.
Чему равен импульс одного фотона?
Общий план решения:
1. Энергия одного фотона.
2. Общее число фотонов.
3. Число фотонов в видимой области спектра.
4. Число фотонов, попадающих в зрачок человека.
Дано:
P 150 Вт
вид 0,012
R 1м
550 нм
d зр 4 мм
N ф, зр ?
p ?
R
Энергия одного фотона: 1 h
Общее число фотонов:
N общ. ф
hc0
P
1
Число фотонов в видимой области спектра:
N вид. ф
P
1
Число фотонов в видимой области спектра, попадающих в зрачок человек:
P d зр
0,012 150
(4 10 3 ) 2
N зр, ф N вид.ф
2
5,38 1013 с 1
34
8
2
Sсф 1 4 R
6,62 10 3 10
4 1
2
S зр
Импульс одного фотона:
6,62 10 34
12,03 10 25 кг м / с
550 10 9
13 1
25
Ответ: N ф. зр 5,38 10 с ; p 12,03 10 кг м / с
p
h
Наименование и величина множителей, используемых в физике для
обозначения единиц измерения.
Множители
Кратные
Дольные
Наименование
тера
гига
мега
кило
милли
микро
нано
пико
Обозначение
Т
Г
М
к
м
мк
н
п
Величина
1012
109
106
103
10-3
10-6
10-9
10-12
ЛАБОРАТОРНЫЙ ПРАКТИКУМ
№
№ раздела
(темы)
1
2
3
4
5
6
7
1.1
1.2
1.4
1.4
1.4
1.6
8
2.4
9
3.1
Наименование лабораторных работ
Теория погрешностей. Простейшие измерения.
Определения ускорения свободного падения.
Исследование центрального удара шаров.
Исследование вращательного движения твердого тела.
Изучение прецессии гироскопа.
Определение моментов инерции твердых тел
Определение коэффициента внутреннего трения
по методу Стокса
Определение отношения удельной теплоемкости при
постоянном давлении к удельной теплоемкости при
постоянном объеме.
Определение электрической емкости конденсаторов.
10
11
3.2
3.3
12
3.4
13
14
15
16
17
18
3.4
3.6
4.2
5.2
5.3
5.3
19
20
5.3
6.1
Определение удельного сопротивления проводника.
Определение ширины запрещенной зоны
полупроводника.
Определение горизонтальной составляющей
напряженности земного магнитного поля.
Определение удельного заряда электрона.
Исследование ферромагнетиков.
Физический маятник.
Определение фокусного расстояния линзы.
Определение длины волны света.
Определение разрешающей способности дифракционной
решетки.
Исследование свойств поляризованного света.
Определение энергии диссоциации бихромата калия.
ПРИМЕР ОФОРМЛЕНИЯ ОТЧЕТА ПО ЛАБОРАТОРНОЙ РАБОТЕ
ОТЧЕТ
по лабораторной работе № 1
ПРОСТЕЙШИЕ ИЗМЕРЕНИЯ
Выполнил студент _________________________________ (Фамилия И..О.)
Учебная группа: ___________________________
Цель работы: определение плотности вещества и ознакомление с методом определения погрешностей при
измерениях.
Приборы и оборудование: весы, штангенциркуль, цилиндр.
Схема установки:
D
ρср
Расчетные
4m формулы:
D 2 h
m 2D h
N
D
h
m
ρист
ρ
m
h
−Δρ
+Δρ
Задача №
9
Фокусное
расстояние
собирающей
линзы 20 см,
расстояние
от предмета
до линзы 10
см, высота
предмета 2
см. Найти
высоту
мнимого
Таблица результатов наблюдений и расчетов:
изображения
. Как
изменится
m, г
Δm, г
Δmсист
D, мм
высота №
изображения
, если
1
предмет
отодвинуть2
от линзы на
расстояние
3
25. см?
ΔD, мм
ΔDсист
h, мм
Δh, мм
СЗ
Вывод (полученный результат):
ρ =
±
кг
3
м
_______________ (дата) ________________________ ( подпись студента)
Δhсист
