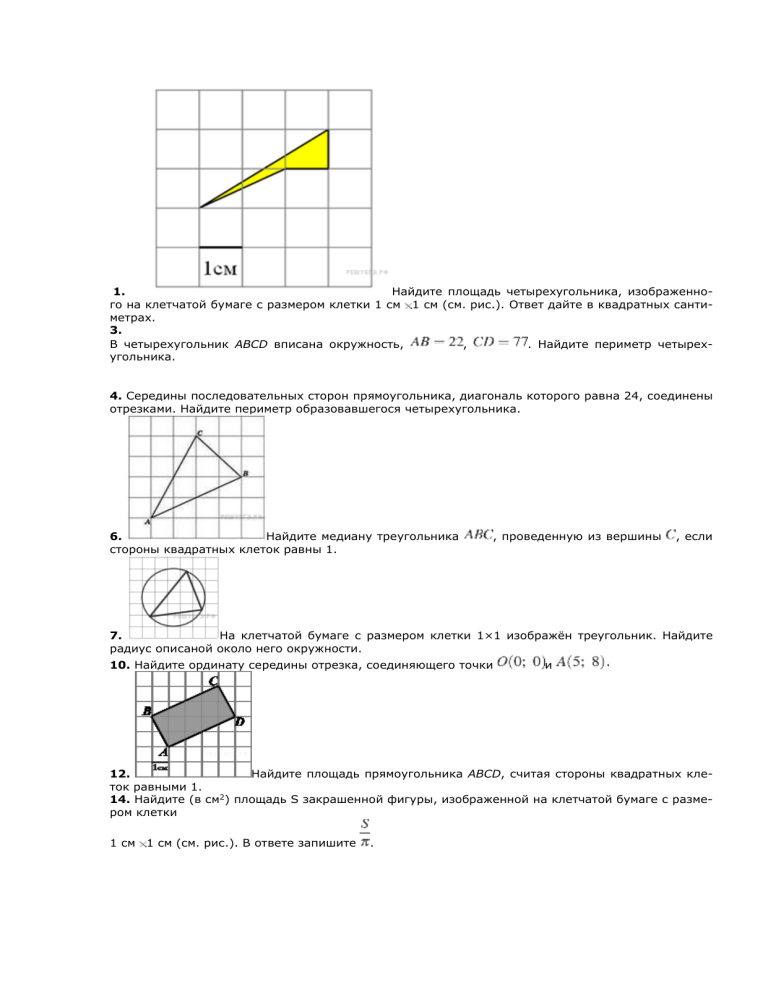
1.
Найдите площадь четырехугольника, изображенного на клетчатой бумаге с размером клетки 1 см 1 см (см. рис.). Ответ дайте в квадратных сантиметрах.
3.
В четырехугольник ABCD вписана окружность,
,
. Найдите периметр четырехугольника.
4. Середины последовательных сторон прямоугольника, диагональ которого равна 24, соединены
отрезками. Найдите периметр образовавшегося четырехугольника.
6.
Найдите медиану треугольника
стороны квадратных клеток равны 1.
, проведенную из вершины
, если
7.
На клетчатой бумаге с размером клетки 1×1 изображён треугольник. Найдите
радиус описаной около него окружности.
10. Найдите ординату середины отрезка, соединяющего точки
и
12.
Найдите площадь прямоугольника ABCD, считая стороны квадратных клеток равными 1.
14. Найдите (в см2) площадь S закрашенной фигуры, изображенной на клетчатой бумаге с размером клетки
1 см 1 см (см. рис.). В ответе запишите
.
17. В треугольнике ABC угол C равен 90°,
. Найдите тангенс внешнего угла при вершине A.
18. В треугольнике ABC угол C равен 90°,
,
. Найдите BC.
19. Радиус окружности, вписанной в равнобедренный прямоугольный треугольник, равен 43.
Найдите гипотенузу c этого треугольника. В ответе укажите
.
21. Большее основание равнобедренной трапеции равно 34. Боковая сторона равна 14. Синус
острого угла равен
. Найдите меньшее основание.
22. В треугольнике
угол равен 90°, высота
равна 20,
. Найдите
.
23. Около окружности, радиус которой равен 1, описан многоугольник, периметр которого равен
8. Найдите его площадь.
24. В параллелограмме
,
,
. Найдите большую высоту параллелограмма.
26. Точка пересечения биссектрис двух углов параллелограмма, прилежащих к одной стороне,
принадлежит противоположной стороне. Меньшая сторона параллелограмма равна 5. Найдите
его большую сторону.
27. В треугольнике
угол равен 90°,
,
. Найдите
.
28. В треугольнике
угол равен 90°, тангенс внешнего угла при вершине равен
,
. Найдите
.
29. Найдите высоту трапеции, в которую вписана окружность радиуса 47.
30. В треугольнике ABC угол C равен 90°,
,
. Найдите
.
33. В основании прямой призмы лежит ромб с диагоналями, равными 6 и 8. Площадь ее поверхности равна 248. Найдите боковое ребро этой призмы.
35. В правильной треугольной пирамиде
точка
— середина ребра
, — вершина. Известно, что
,а
. Найдите площадь боковой поверхности.
41.
Найдите расстояние между вершинами
раженного на рисунке. Все двугранные углы многогранника прямые.
44. Задание 8 № 25623.
и
многогранника, изоб-
Найдите площадь поверхности многогранника, изображенного на рисунке (все двугранные углы
прямые).
46. На ребре
между прямыми
куба
и
отмечена точка
так, что
Найдите угол
48. В прямоугольном параллелепипеде ABCDA1B1C1D1 найдите угол между плоскостью AA1C и
прямой A1B, если AA1 = 3, AB = 4, BC = 4.
49. В правильной треугольной пирамиде MABC с основанием ABC стороны основания равны 6, а
боковые рёбра 8. На ребре AC находится точка D, на ребре AB находится точка E, а на ребре AM
— точка L. Известно, что СD = BE = LM = 2. Найдите площадь сечения пирамиды плоскостью,
проходящей через точки E, D и L.
50. . Ребро куба ABCDA1B1C1D1 равно 1. Найдите расстояние от вершины B до плоскости ACD1.
51. Дан равнобедренный треугольник ABC с основанием AC. Вписанная в него окружность с центром O касается боковой стороны BC в точке P и пересекает биссектрису угла B в точке Q.
а) Докажите, что отрезки PQ и OC параллельны.
б) Найдите площадь треугольника OBC, если точка O делит высоту BD треугольника в отношении
BO : OD = 3 : 1 и AC = 2m.
55. Две окружности касаются внешним образом в точке K. Прямая AB касается первой окружности в точке A, а второй — в точке B. Прямая BK пересекает первую окружность в точке D, прямая
AK пересекает вторую окружность в точке C.
а) Докажите, что прямые AD и BC параллельны.
б) Найдите площадь треугольника AKB, если известно, что радиусы окружностей равны 4 и 1.
