ГЕОМЕТРИЯ, 10 класс
Ответы и критерии, Март 2010
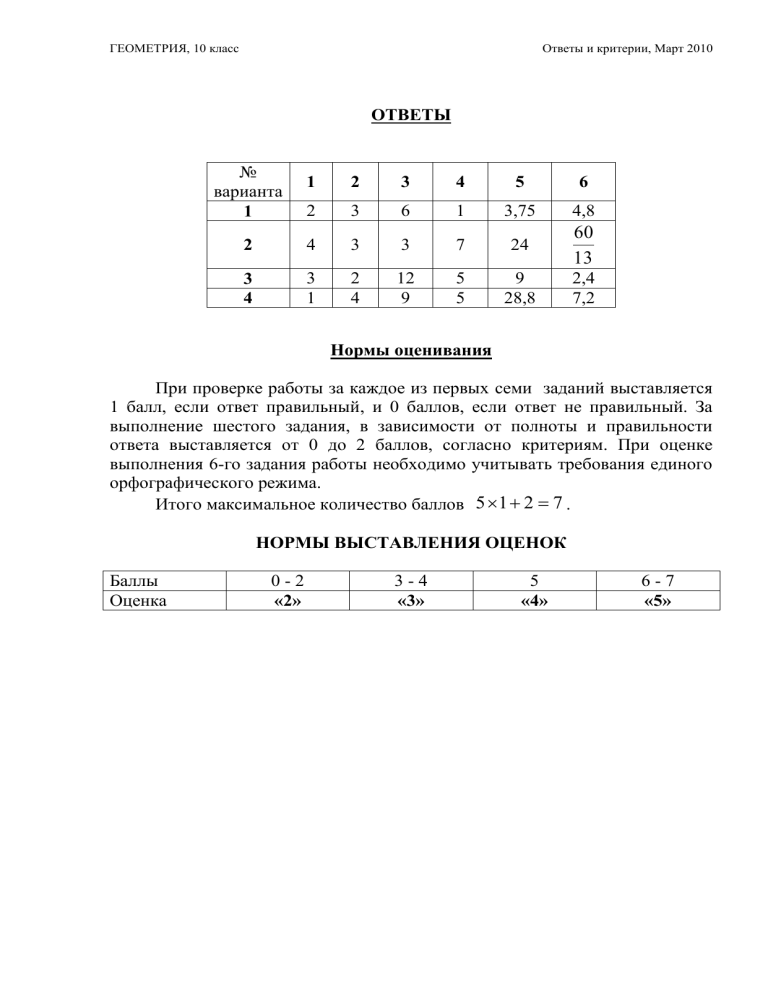
ОТВЕТЫ
№
варианта
1
1
2
3
4
5
6
2
3
6
1
3,75
4,8
2
4
3
3
7
24
60
13
3
4
3
1
2
4
12
9
5
5
9
28,8
2,4
7,2
Нормы оценивания
При проверке работы за каждое из первых семи заданий выставляется
1 балл, если ответ правильный, и 0 баллов, если ответ не правильный. За
выполнение шестого задания, в зависимости от полноты и правильности
ответа выставляется от 0 до 2 баллов, согласно критериям. При оценке
выполнения 6-го задания работы необходимо учитывать требования единого
орфографического режима.
Итого максимальное количество баллов 5 1 2 7 .
НОРМЫ ВЫСТАВЛЕНИЯ ОЦЕНОК
Баллы
Оценка
0-2
«2»
3-4
«3»
5
«4»
6-7
«5»
ГЕОМЕТРИЯ, 10 класс
Ответы и критерии, Март 2010
КРИТЕРИИ ОЦЕНИВАНИЯ ЗАДАНИЙ № 6
Варианты № 1, 4
№ 1 В треугольнике ABC синус угла B
равен 2 , AB 20 . SA 6 - отрезок
5
перпендикулярный плоскости данного
треугольника. Найдите расстояние от
точки A до плоскости (SBC).
Ответ: 4,8
S
H
A
C
D
B
Решение.
1). В плоскости ABC проведем высоту AD. Т.к. SA ABC , то по
теореме о трех перпендикулярах следует, что SD BC .
Следовательно, BC ASD ASD BSC . В плоскости
ASD из точки A опустим перпендикуляр AH на SD. AH SBC искомое расстояние.
2). В прямоугольном V ABD AD AB sin ABD 20 2 8 . В
5
SD AS 2 AD 2 36 64 10 .
VASD
Следовательно, AH AS AD 6 8 4,8
SD
10
Ответ: 4,8
прямоугольном
Баллы
2
1
0
Критерии оценки выполнения задания № 6
Приведена верная последовательность шагов решения.
Верно и обосновано искомое расстояние.
Все преобразования и вычисления выполнены верно.
Получен верный ответ.
Верно и обосновано искомое расстояние.
Возможно решение не доведено до конца или допущена одна
негрубая вычислительная ошибка или описка, в результате
которой, получен неверный ответ.
Все случаи решения, которые не соответствуют вышеуказанным
критериям выставления 1-2 баллов
Замечание. Допустимы другие методы решения.
ГЕОМЕТРИЯ, 10 класс
Ответы и критерии, Март 2010
R
№ 4 RA 9 - отрезок перпендикулярный
плоскости треугольника ABC. Найдите
расстояние от точки A до плоскости (RBC),
если CR 50 , sin BCR 0, 9 .
3
Ответ: 7,2
H
A
C
D
Решение.
1). В плоскости ABC проведем высоту AD.
Т.к. RA ABC , то по теореме о трех
B
перпендикулярах следует, что RD BC .
Следовательно, BC ARD ARD BRC . В плоскости
ARD из точки A опустим перпендикуляр AH на RD. AH RBC искомое расстояние.
2). В прямоугольном VRCD RD RC sin RCD 50 9 15 . В
3 10
2
2
AD RD AR 225 81 12 .
V ARD
Следовательно, AH AR AD 9 12 7, 2 .
RD
15
Ответ: 7,2
прямоугольном
Варианты № 2, 3
№ 2 В треугольнике ABC сторона BC 1.
отрезок
перпендикулярный
QA 5
плоскости данного треугольника. Найдите
расстояние от точки A до плоскости (QBC),
если площадь треугольника BQC равна 6,5.
Ответ: 60
13
Q
H
A
C
D
B
Решение.
1). В плоскости ABC проведем высоту AD. Т.к. QA ABC , то по
теореме о трех перпендикулярах следует, что QD BC .
Следовательно, BC AQD AQD BQC . В плоскости
AQD из точки A опустим перпендикуляр AH на QD. AH QBC искомое расстояние.
ГЕОМЕТРИЯ, 10 класс
Ответы и критерии, Март 2010
2 6, 5
В
1 BC QD QD
13 .
VBQC
2
1
2
2
V AQD
AD QD AQ 169 25 12 .
AQ AD 5 12 60
AH
.
QD
13
13
Ответ: 60
13
2). S
Баллы
2
1
0
прямоугольном
Следовательно,
Критерии оценки выполнения задания № 6
Приведена верная последовательность шагов решения.
Верно и обосновано искомое расстояние.
Все преобразования и вычисления выполнены верно.
Получен верный ответ.
Верно и обосновано искомое расстояние.
Возможно решение не доведено до конца или допущена одна
негрубая вычислительная ошибка или описка, в результате
которой, получен неверный ответ.
Все случаи решения, которые не соответствуют вышеуказанным
критериям выставления 1-2 баллов
Замечание. Допустимы другие методы решения.
№ 3 Площадь треугольника ABC равна 3,
BC 2 . PA 4 - отрезок перпендикулярный
плоскости данного треугольника. Найдите
расстояние от точки A до плоскости (PBC).
Ответ: 2,4
P
H
A
C
D
Решение.
B
1). В плоскости ABC проведем высоту AD.
Т.к. PA ABC , то по теореме о трех перпендикулярах следует,
что PD BC . Следовательно, BC APD APD BPC . В
плоскости APD из точки A опустим перпендикуляр AH на PD.
AH PBC - искомое расстояние.
2). S V ABC 1 BC AD AD 2 3 3 .
В прямоугольном
2
2
PD AD 2 AP 2 9 16 5 .
V APD
Следовательно,
AH AP AD 4 3 2, 4 .
PD
5
Ответ: 2,4
